A New Hyperspectral Spherical-Cavity Absorption Meter
David R. Dana and Robert A. Maffione, HOBI Labs, Inc.
Adapted from a Poster Presented at Ocean Sciences 2006
Honolulu, Hawaii, Feb 20-24, 2006
(Poster in Corel Draw format)(Paper in PDF Format)

a-Sphere
The world's first and only integrating-sphere spectrophotometer that measures the absorption coefficient of ocean waters in-situ. a-Sphere is rated to 600 m depth.
How do you measure spectral light absorption by ocean water-or any other liquid? How do you accurately determine the spectral absorption coefficient, in inverse meters (m-1), over the full spectrum? The only widely accepted method is to use an integrating sphere. An integrating sphere with high diffuse reflectivity renders insignificant the scattering by suspended solids in the liquid. It also increases the absorption path length, thereby increasing the instrument sensitivity and accuracy. There simply is no better approach for measuring the absorption coefficient of any liquid. Yet until now this approach has not been available in a commercial instrument. The engineering challenge has been in how to implement this approach in a practical instrument. The scientific challenge has been in how to calibrate such an instrument.
HOBI Labs has developed an integrating sphere absorption meter for both in-water (depths to 600 m) and laboratory applications. This revolutionary instrument is called the a-Sphere. The laboratory version, which has additional spectral capabilities, is called the HyperSphere. Moreover, we have developed an accurate and scientifically verifiable calibration methodology.
Comparative Absorption Measurement Methods
Laboratory Spectrophotometers
Laboratory spectrophotometers typically use a very small measurement volume, or dried samples deposited on filter paper. In some cases a solid or encapsulated liquid sample is placed in an integrating sphere acting as an uncalibrated light collector. To achieve adequate sensitivity the samples must be concentrated after being collected in the field. The necessary procedures are cumbersome, time-consuming, subject to contamination and chemical degradation, and obviously inappropriate to in-situ use. Finally, the results are typically expressed in terms of absorbance or absorptance, quantities that are not applicable to geometries other than the measurement apparatus.
Reflecting Tube
This variation on an in-situ transmissometer attempts to minimize scattering errors by enclosing the sample in a highly reflecting tube, and using a wide-angle receiver that collects both direct and scattered light. However a significant portion of the scattered light is still lost, and the amount lost must be estimated and corrected for. Also, the absorption over the typical 25 cm path is still small enough in clear water that some users find it necessary to bring a source of highly purified water into the field for frequent comparison measurements.1
Light entering through an aperture reflects off the wall many times, distributing the light uniformly over the internal surface. More importantly for absorption measurements, the multiple reflections in an integrating sphere cause photons to traverse a total distance much greater than the dimensions of the cavity. This greatly increases the effective path length and therefore the sensitivity of the measurement. a-Sphere’s 10 cm sphere gives effective path lengths of up to 2 meters, as shown in Figure 1.
An integrating sphere has walls with high diffuse reflectivity. At the same time, the integrating cavity’s sensitivity to scattering is very low, because the cavity captures and reflects scattered photons just as efficiently as unscattered ones. The only error introduced by scattering is a slight increase in the total path length traversed by scattered photons, but this error is not significant in most practical cases. Figure 2 shows a-Sphere’s negligible scattering sensitivity.
Earlier Integrating Cavity Absorption Measurements
Fry, Kattawar and Pope first demonstrated the viability of using a non-spherical integrating cavity for absorption measurements in the laboratory.2 Pope and Fry refined this approach to measure the absorption of pure water.3,4 However their apparatus was developed specially for those measurements and is not suitable for use outside the laboratory. Kirk has extensively modeled the performance of integrating cavities and concluded that optimum performance is obtained with an isotropic light source in the center of a sphere.5,6 However that approach entails major engineering challenges, and our work indicates it is not necessary for practical purposes.
Return to table of contents
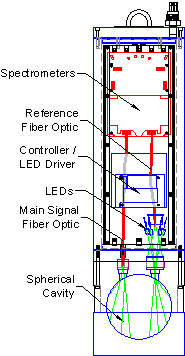
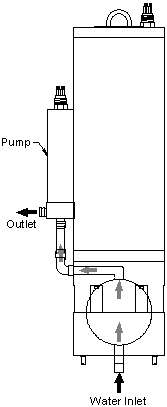
Figure 3: Schematic View
The in-situ a-Sphere and the bench-top HyperSphere have the same essential features, which are shown at right.
Integrating Sphere
The sphere, key to the instrument&rsquos;s performance, is made of solid plastic that has high diffuse reflectivity. But unlike materials such as Spectralon™, it is impervious to water and other substances, so the fluid under test can be pumped directly into the sphere. The sphere is shielded against external light by an opaque shell, and divided into two hemispheres, one of which is removable for easy cleaning. The fluid inlet and outlet are configured for easy connection to a submersible pump, and a streamlined flow path prevents trapping of bubbles.
Light Source
a-Sphere is also distinguished by its solid-state light source. An array of light-emitting diodes provides efficiency, reliability, and ease of electronic control. By carefully selecting a set of LEDs and adjusting their drive, we balance the spectral output to complement the response of the detector, levelling the response over the full 360 to 850 nm range (Figure 4). The LEDs can be switched on and off under instrument control to measure and compensate for dark offsets, or for special applications including fluorescence measurement. HyperSphere offers an optional deuterium light source that extends the wavelength range down to 200 nm.
Optics
The light source illuminates the sphere interior through a 1 cm aperture with a sealed fused silica window. The received signal is sensed by an optical fiber looking through a second, similar window. A second fiber views the output of the light source before it enters the sphere, to provide a reference measurement.
Detectors
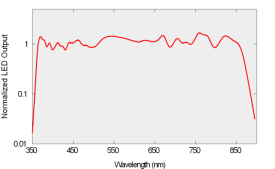
Figure 4: Light source spectrum
A sensitive CCD spectrometer measures the radiance in the sphere with spectral resolution of about 0.3 nm per pixel from 200 to 850 nm. A second, identical spectrometer measures the light source output, to correct for any changes in its output. Variable integration time allows the spectrometers to accommodate a very wide range of signals. Typical integration times in most natural waters are 100 ms or less.
Electronics
An intelligent controller regulates the light source(s), controls the signal and reference spectrometers, and receives and interprets commands. The command interpreter can execute arbitrary sequences of commands stored in files, including timed sequences for scheduled data collection over long periods. Data can be stored in high-capacity flash memory, transmitted in real time, or both.
Return to table of contents
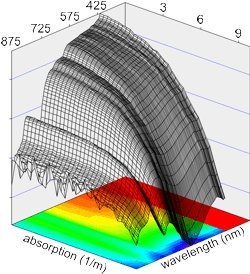
Figure 6: Calibration Data
Signal versus wavelength and absorption
Rather than depend on mathematical models of sphere performance, we calibrate a-Sphere by directly measuring its signal, S(a,λ), in response to known absorptions.
Dye Absorption Standards
To produce solutions with known absorption, we use nigrosin dye in carefully measured concentrations. We first measure the dye-specific absorption coefficient of a concentrated dye solution, a*(λ) with a spectrophotometer. Knowing a*(λ), we can calculate the absorption coefficient, a(λ), of more dilute solutions that are suitable for a-Sphere’s high sensitivity.
Measuring S(a,λ)
Varying the dye concentration over a wide range while recording the a-Sphere output, we acquire a set of S(a,λ) values like that shown in figure 6. Typical curves of S(a) for individual wavelengths are also shown in figure 2.
From the S(a,λ) dataset we can observe the inverse function, a(S,λ). For each wavelength we fit a polynomial to a(S). These fitting functions can then be used to convert measured values of S to calibrated absorptions.
Calibration Maintenance: No Pure Water Required
I-Spehre calibration values are normalized by Sd(λ), the output of the instrument when its sphere is empty and dry. Because of the properties of the integrating sphere, small changes in instrument response have proportional effects on “dry” and “wet” readings. Therefore the calibration can be easily maintained in the field or laboratory by periodically recording and normalizing by the dry-sphere response. This is vastly easier than transporting and maintaining a source of pure water. The a-Sphere’s split-sphere design makes it especially easy to clean and dry (Figure 5).
Return to table of contents
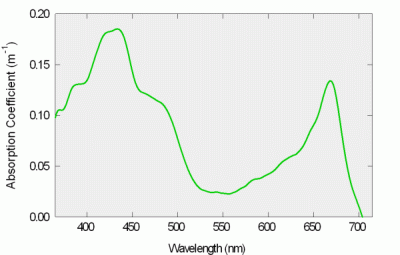
Figure 7: Plant extract absorption spectrum
The a-Sphere was used to measure a suspension of plant leaf extracts, whose absorption spectrum is shown in Figure 7. In contrast to spectrophotometer measurements, no special preparation of the sample is required for measurements like these. Scattering from suspended particles does not affect the measurement, and the results are provided in transferable units of inverse meters (m-1) rather than dimensionless absorbance. The spectrum is dominated by chlorophyll's characteristic absorption. Such measurements are abundant in the literature, but are typically not calibrated in inverse meters, nor measured as quickly and easily as with the a-Sphere.
Return to table of contents
Lake Profiling
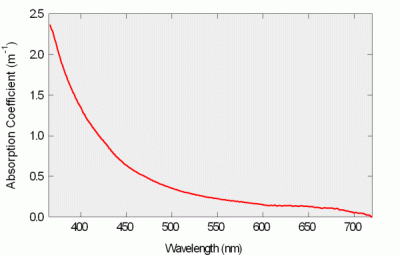
Figure 9: Absorption Spectrum of Lake Water
We deployed the a-Sphere in Lake Washington, profiling in water up to 65 m deep, with water continuously pumped through the sphere. In the photo at left, a filter is attached to the water inlet to remove particles from the water and allow measurement only of dissolved matter. In both cases the spectrum was dominated by colored dissolved organic matter (CDOM), and the Lake showed essentially no stratification, so the absorption spectrum remained as shown below throughout the profiles.
Puget Sound Time Series
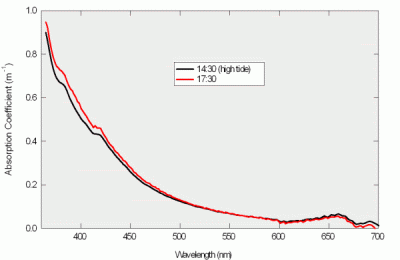
Figure 10: Puget Sound absorption spectra
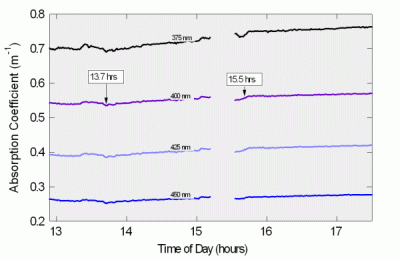
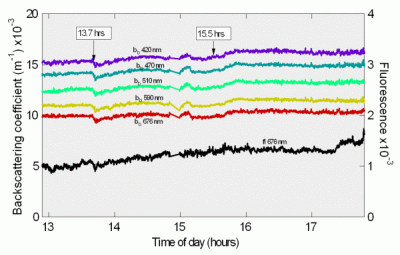
Figure 11: Puget Sound Time Series
Top: UV-Blue absorption
Bottom: Backscattering and fluorescence
(click to enlarge)
We deployed an a-Sphere, simultaneously with a HydroScat-6 spectral backscattering sensor/fluorometer, in Puget Sound for a 5-hour time series. Representative spectra are shown in Figure 10. Like that of Lake Washington, this spectrum shows a major CDOM component, with the absorption rapidly increasing at shorter wavelengths. However Figure 10 also clearly shows a significant contribution from Chlorophyll, as indicated by the shoulders at 380 and 420 nm, and the peak at 670 nm.
Although the water changed only slightly during the time series, the a-Sphere clearly detected the changes. Over the course of the experiment there was a slight increase in absorption at short wavelengths. Figure 10 shows one spectrum measured at high tide, at which point the absorption was near its minimum, and one near the end of the experiment, after the tide had lowered about 1.5m. The change in spectrum implies that the CDOM increased as the outgoing tide drew water from shallower areas of the Sound.
Figure 11 shows absorption versus time at four wavelengths in the UV-blue region, since those wavelengths showed the greatest variation. These data show a small but steady rise in absorption. This corresponds to a similar rise in scattering and fluorescence recorded by the HydroScat-6, shown below in Figure 12. Note the small events at 13.7 and 15.5 hours, which also appear in the scattering data. Though very small, they are well within the measurement capability of the a-Sphere. With other absorption meters, one would need to consider whether these small absorption events were simply caused by scattering interference. a-Sphere’s immunity to scattering allows us to conclude that they are genuine.
Return to table of contents
- WET Labs, Inc., “AC-9 Protocol”
- Fry, E.S., G.W. Kattawar and R.M. Pope, “Integrating cavity absorption meter,”Appl. Opt. 31, 2055-2065 (1992)
- Pope, R.M., “Optical absorption of pure water and sea water using the integrating cavity absorption meter,” Ph.D. dissertation, Texas A&M University, College Station, TX (1993)
- Pope, R.M. and E.S. Fry, “Absorption spectrum (380-700nm) of pure water. II. Integrating cavity measurements,” Appl. Opt. 36, 8710-8723 (1997)
- Kirk, J., “Modeling the performance of an integrating-cavity absorption meter: theory and calculations for a spherical cavity,” Appl. Opt. 34, 4397- (1995)
- Kirk,J., “Point-source integrating-cavity absorption meter: theoretical principles and numerical modeling,” Appl. Opt. 36, 6123-6128 (1997)